brickqert.blogg.se - Quadratic inequalities

#Quadratic inequalities pdf

In the last example, the parabola opened upward and in the next example, it opens downward.

#Quadratic inequalities pdf

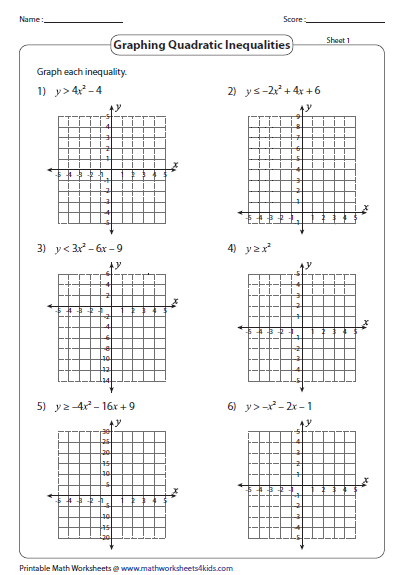
These math worksheets should be practiced regularly and are free to download in PDF formats. Step by step guide to solve Solving Quadratic Inequalities. Write the quadratic inequality in standard form. Download Quadratic Inequalities Worksheet PDFs We use quadratic inequalities calculating areas, determining a product's profit or formulating the speed of an object. Name: Math Worksheets Date: So Much More Online Please visit: Solving Quadratic Inequalities Solve each quadratic inequality.

Solving Quadratic Inequalities worksheets is helpful as they are used to compare numbers and determine the range or ranges of values that satisfy the conditions of a given variable. Quadratic Inequalities is an essential concept in mathematics. Benefits of Quadratic Inequalities Worksheets Fogel and Chellapilla’s Blondie24 was published over the course of two papers. It shows the data which is not equal in graph form. An equation is a statement that asserts the equality of two expressions and a linear inequality is an inequality which involves a linear function. In order to solve a quadratic inequality, it is necessary to solve the corresponding quadratic equation.

ax2 + bx + c < 0 ax2 + bx + c > 0 ax2 + bx + c 0 ax2 + bx + c 0 You can solve quadratic inequalities using algebraic methods or graphs.

Step 3: Shade the x-values that produce the desired. Step 4: Using the graph or otherwise, we need to determine the inequality symbols that will make the solutions found in step 2 satisfy the inequality.Įxplore the examples with answers shown below to understand the application of these steps with real problems.In quadratic inequalities worksheets, we learn that a quadratic inequality is an equation of second degree that uses an inequality sign instead of an equal sign. 142 Chapter 3 Quadratic Equations and Complex Numbers Solving Quadratic Inequalities in One Variable A quadratic inequality in one variable can be written in one of the following forms, where a, b, and c are real numbers and a 0. Step 1: Place the inequality in standard form with zero on one side.

Values below the x-axis are less than 0, and values above the x-axis are greater than 0.

If the quadratic term is negative, the parabola opens down. Quadratic Inequalities Given 3 x 2 > -x + 4 Rewrite the inequality with one side equal to zero.

Sketch the graph of the quadratic function.

If we have a positive quadratic term, the parabola opens up and is U-shaped. First replace the inequality sign by and solve the quadratic equation.

Alternatively, we can solve without a graph by considering the following: This resulted from the fact that, in each case we found two solutions to the corresponding quadratic equation ax 2 + bx + c 0. Step 3: Sketch a simple graph of the function $latex y=ax^2+bx+c$ to determine the solution. The solutions of the quadratic inequalities in each of the previous examples, were either an interval or the union of two intervals. To achieve this, we can solve the quadratic equation by factoring $latex ax^2+bx+c=0$ and find the x values.

Step 2: Identify where the graph of $latex y=ax^2+bx+c$ intersects the x-axis. The “<” sign could be different depending on the problem. Step 1: Simplify and write the inequality in the form $latex ax^2+bx+c<0$.

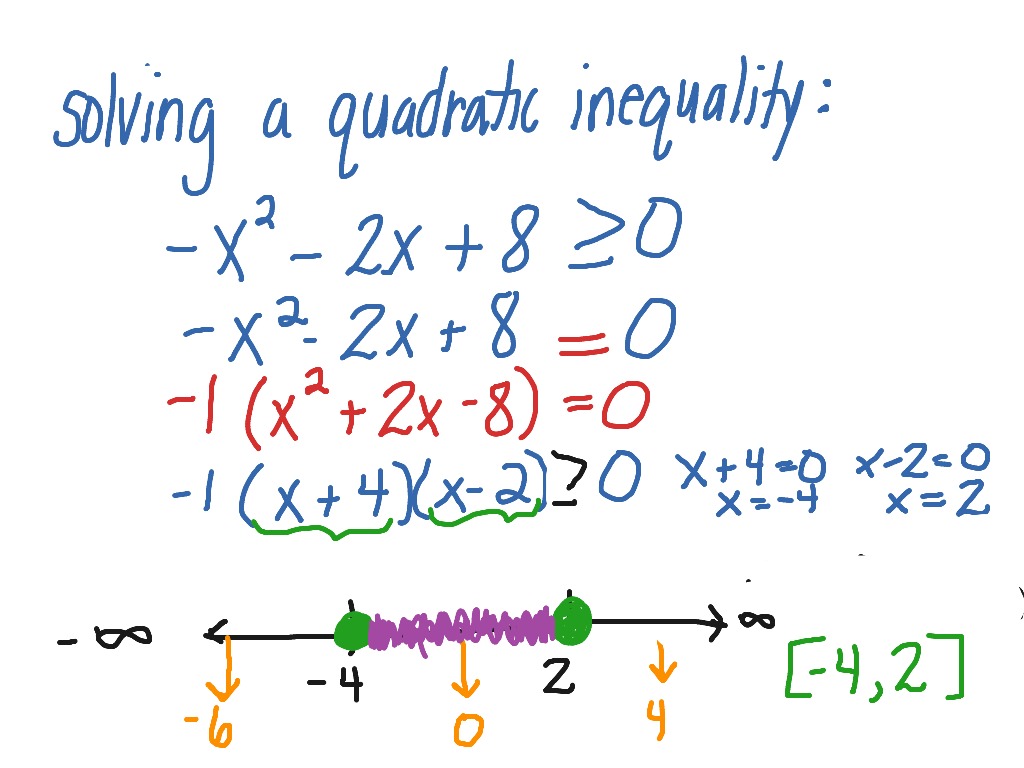
However, the procedure for solving the problem will be exactly the same for strict inequalities and inequalities that are not strict.

To solve quadratic inequalities, we can follow the following steps: Some examples of quadratic inequalities are: x2 + 7x -3 > 3x + 2 2x2 - 8 5x2 x + 7 < x2 -3x + 1 Here the first and third are strict inequalities, and the second one is not. A quadratic inequality is of the form: a x 2 + b x + c > 0 Where a 0, and our > can be replaced with any inequality symbol.